|
エンゲルスの、『自然の弁証法』において、量と質の相関に関して、以下の記述が、見出されます。 「質的な変化はただ物質または運動(いわゆるエネルギー)の量的な加減によってのみ起こりうる」 量から質への転化に関して、その最も簡単な実例は、酸素とオゾンおいて、見出されます。 酸素分子とオゾンは、共に、酸素原子から構成されます。 分子式 O2 の酸素は、酸素原子の個数は、2個です。 分子式 O3 のオゾンは、酸素原子の個数は、3個です。 酸素分子とオゾンの相違は、酸素原子の個数の、量的な相違です。 他方、質な相違は、酸素分子は無臭であり、オゾンは匂いがあります。 運動あるいはエネルギーの形態変化として、熱を力学的運動に変化させる、蒸気機関があります。 また、摩擦火は、力学的運動が、熱に変化する、事例です。 運動(いわゆるエネルギー)の量的な加減による、質的な変化は、水の沸騰において、見出されます。 水は、標準気圧のもとでは、摂氏零度で液体状態から固体状態に、摂氏100度で液体状態から気体状態に、移行します。 この二つの転換点で、温度のたんなる量的変化が、水の状態の質的変化を、呼びおこします。 融点や沸点は、「量的な増減がある特定の結節点で質的飛躍を引きおこす」、結節点と呼ばれています。 『資本論』の「相対的剰余価値の生産」では、協業、分業とマニュファクチュア、機械と大工業の分野で、 量的変化が質を変化させ、質的変化が量を変化させる、無数の事例が、指摘されています。 しかし、質的変化が量を変化させる現象の例は、『自然の弁証法』には、見出されません。 『自然の弁証法』では、以下の記述が、見出されます。 「もしも質のあらゆる区別と変化とを量的な区別と変化とに帰着させうるものとすれば、われわれは必然的に次の命題に到達せざるをえない。すなわち、物質はすべて同一の最小粒子からなりたっていること、また物質をつくりあげている化学的諸元素のすべての質的区別は、これらの最小の粒子が集まって原子となるさいのそれら粒子の個数と場所的配置とのうえでの量的区別によって生じたものである、という命題がそれである。しかしわれわれはまだとてもそこまではいっていないのである。」 ここでは、量と質に関する命題が、最小の粒子との関連で、言及できる段階でないことが、表明されています。 『自然の弁証法』が執筆された1880年頃は、最小の粒子として、電子や陽子は、認識されていません。 現在は、電子と陽子が、原子や分子の化学的な性質に関与する、最小な粒子として、知られています。 原子中の電子の存在は、1902年以降に、認識されています。 シュレーディンガーは、1926年に、原子や分子の世界における、基礎的な方程式を、提唱しました。 ニールス・ボーアは、1913年に、水素原子のエネルギー準位を、理論的に、解明しました。 量子力学・量子化学は、シュレーディンガーの方程式を、原子や分子に適用する研究として、発展しています。 電子計算機の発展は、量子化学の手法を用いて、原子や分子の性質の、理論的な解明を、可能にしました。 筆者は、1990年代に、量子化学者として、分子の電子状態・分子構造・振動状態などの、研究を行いました。 研究の成果は、学術論文として、J.Chem.Phys. などに、掲載されています。 ここでは、研究の成果を考慮して、分子における量と質に関して、以下の課題を、検討します。 「質のあらゆる区別と変化とを量的な区別と変化とに帰着させうる」か、検討します。 最小の粒子としての、電子との関連で、量と質との命題に関して、検討します。 分子は、複数の元素で、構成され、元素の組成比を表す、分子式で区別されます。 メタン, エチレン, ベンゼンは、いずれも、炭素と水素から、構成されます。 分子式 は、メタンが CH4、エチレンは C2H4、ベンゼンは C6H6 です。 分子の性質として、沸点は、メタンが -162 ℃、エチレンは -103.7 ℃、ベンゼンは 80.1℃ です。 分子式が異なれば、分子の性質が、異なります。 これらの分子の性質は、分子を構成する、炭素と水素の数に、相関します。 同一の性質をもった分子は、同一の分子式を、有しています。 しかし、同一の分子式を有する分子でも、異なった性質を示す分子が、見出されます。 n-ブタンとiso-ブタンは、いずれも、C4H10 の、分子式です。 しかし、沸点が異なり、n-ブタンが -0.5℃、iso-ブタンは -11.7 ℃ です。 沸点の相違は、下図に示す、分子構造( 分子の形状 )の相違に、帰着できます。 分子構造は、原子間相互の、結合状態を図示する、下図の構造式で、表示できます。 分子の結合状態の相違により、電子密度が異なり、分子間力が異なり、沸点の相違が生じます。 ここでは、沸点(量)の相違は、分子の結合状態(質)の相違に、起因します。 下図の、二つの分子は、構造異性体と、呼ばれています。 構造異性体は、結合の対をなす原子( C-C, C-H )に関して、組み合わせが、異なっています。 構造異性体
シス-1,2-ジクロロエチレンとトランス-1,2-ジクロロエチレンの分子式は、C2H2Cl2です。 沸点は、シス-1,2-ジクロロエチレンが 60.3℃、トランス-1,2-ジクロロエチレンは 47.5 ℃ と、異なります。 この二つの分子は、下図の構造式で示される、シス型とトランス型の、幾何異性体です。 二つの分子は、結合の対をなす原子に関して、同一の組み合わせです。 同一の平面上の C-Cl 結合に着目すると、シス型は同じ方向に、トランス型は反対方向に、位置しています。 ここでは、沸点の相違は、分子構造の幾何学的な相違に、起因します。 幾何異性体
アラニンは、生体を構成するタンパク質の、アミノ酸として、知られています。 アミノ酸は、光学的な性質が異なる、L体とD体の二種類が、知られています。 L体とD体のアミノ酸は、直線偏光に対する、旋光性が異なります。 この相違は、下図に示す、-NH2 などの官能基の立体配置の相違に、起因します。 これらの立体配置は、互いに鏡像の関係にあり、光学異性体(鏡像異性体)と、呼ばれています。
物質の性質の違いは、酸素やオゾンのように、分子式( O2, O3 )の相違に、関連します。 しかし、ジクロロエチレンのように、同一の分子式を有する物質では、分子の様々な構造式と、関連します。 メタン, チレン, ベンゼンは、下図の構造式を有し、上記のいずれの異性体も、存在しません。
ここでは、これらの分子を対象に、分子に関する、量と質の相関を、検討します。 分子は、複数の陽子と、複数の電子から、構成されます。 原子がお互いに接近し、原子間の化学結合を生じ、分子を、形成します。 化学結合に関与する電子は、価電子( valence electron )と呼ばれ、最外殻の電子軌道が、関与します。 分子でも、質(波動関数)と量(エネルギー)の関係が、シュレーディンガー方程式より、解明できます。 HΨ=EΨ H:ハミルトニアン Ψ:波動関数 E:エネルギー ハミルトニアンHは、ポテンシャルエネルギーと運動エネルギーに関する、演算子です。 ハミルトニアンを通して、各々の原子核の位置・質量・陽子数が、波動関数とエネルギーに、反映します。 複数の陽子と電子で構成される系では、厳密なシュレーディンガー方程式の解を得ることは、不可能です。 しかし、ボルン-オッペンハイマー近似を用いると、分子に関する、初歩的な認識が、可能になります。 さらに、現在では、種々の近似法が、開発され、電子計算機を利用して、分子の解明が、試みられています。 ボルン-オッペンハイマー近似では、分子の運動は、電子の運動と原子核の運動に、分離します。 分子の波動関数は、電子の波動関数・振動の波動関数・回転の波動関数に、分離できます。 分子のエネルギーは、電子のエネルギー・振動のエネルギー・回転のエネルギーの和で、近似できます。 電子の運動は、電子の波動関数で表現され、その固有エネルギーは、可視光線からX線の領域に、相当します。 原子核の振動は、振動の波動関数で表現され、その固有エネルギーは、赤外線の領域に、相当します。 分子の回転運動は、回転の波動関数で表現され、その固有エネルギーは、マイクロ波の領域に、相当します。 電子の波動関数は、分子軌道・MO ( Molecular Orbital ) を用いた、電子配置によって、記述されます。 分子軌道は、s, p, d 軌道などの原子軌道の線形結合を用いて、記述されます。 この方法は、LCAO MO ( Linear Combination of Atomic Orbitals MO ) 法と、呼ばれています。 線形結合の係数は、ハートリーフォック ( HF ) の SCF ( Self-Consistent Field ) 法を用いて、決定されます。 電子配置は、様々な分子軌道に対し、電子を配列することによって、得れます。 基底状態は、最もエネルギーが低い電子配置に、対応します。 HFSCF法より精度の高い、波動関数は、CI法( configuration interaction method )によって、得れます。 CI法の波動関数は、複数個の電子配置の線形結合として、記述されます。 分子は、複数の原子核で構成され、様々な原子核の空間配置・分子構造を、有します。 様々な分子構造は、核間距離や結合角など、分子の内部座標で、記述されます。 電子の波動関数(質)より、様々な原子核の配置に対応した、電子の固有エネルギー(量)が、求まります。 電子の固有エネルギーより、分子の内部座標に対応する、ポテンシャルエネルギーの曲面(質)が、得れます。 ポテンシャルエネルギーの曲面には、エネルギーの極小値(量)が、見いだせます。 エネルギーの極小値は、分子構造の量( 結合距離や結合角 )や質(形状)を、与えます。 下図は、最も簡単な分子である、水素分子 H2 に関し、核間距離に対応する、ポテンシャルエネルギーです。 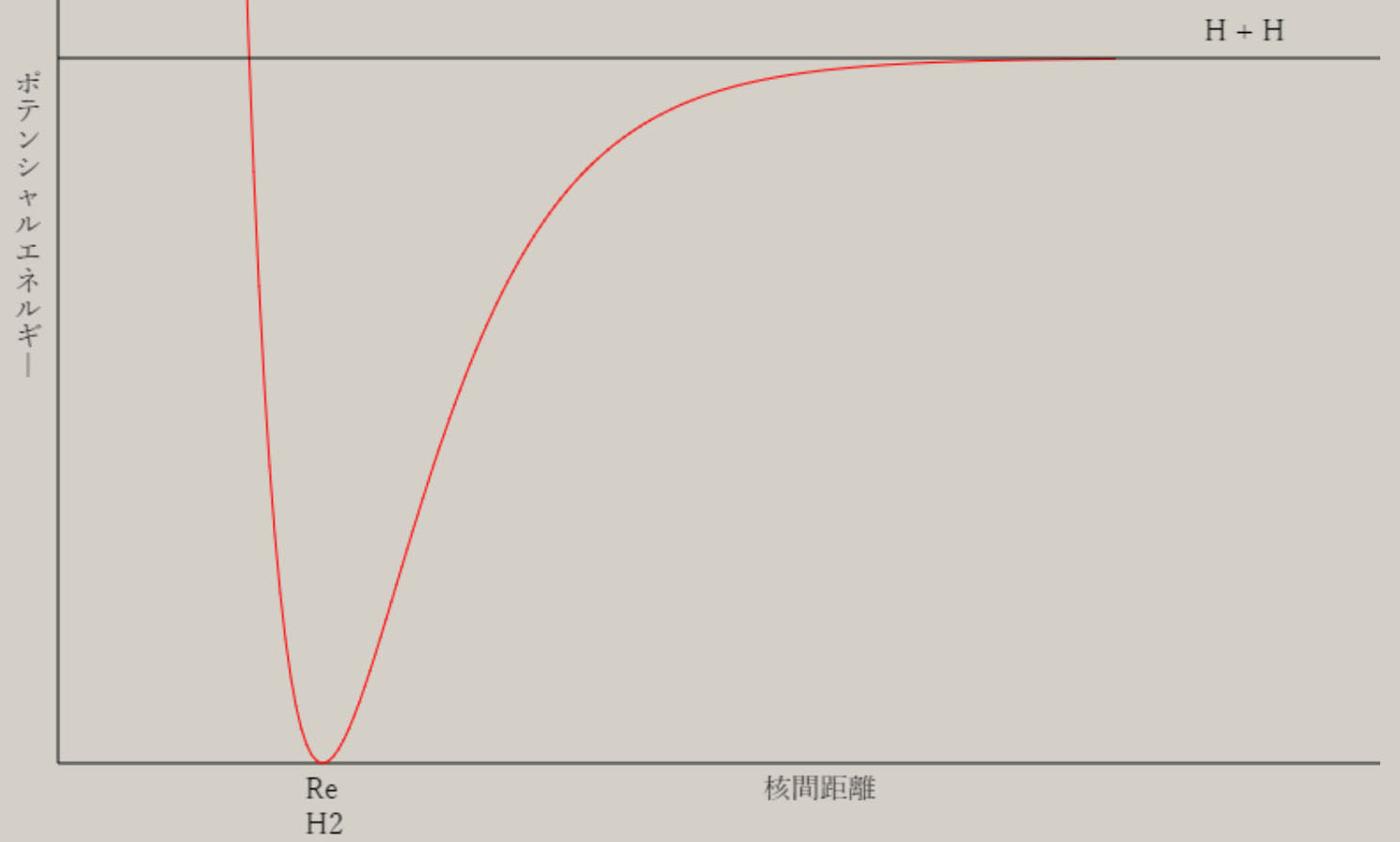 核間距離が大きな領域では、水素分子が、二個の水素原子に、解離しています。 水素原子が接近すると、ポテンシャルエネルギーが、減少し、水素分子を、形成します。 ポテンシャルエネルギーの極小値の核間距離が、水素分子の結合距離・平衡核間距離(Re)です。 水素分子の平衡核間距離は、0.74 Å ( 10-8 cm )です。 平衡核間距離(量)は、ポテンシャルエネルギーの形状(質)と、関連します。 水素分子の解離状態と、平衡核間距離との、ポテンシャルエネルギーの差が、水素分子の、結合エネルギーです。 水素分子の結合エネルギーは、4.74 eV ( electron volt, 電子ボルト) です。 核間距離が 0.8*Re と 1.5*Re では、ポテンシャルエネルギーが、結合エネルギーの、1/2 になります。 核間距離が、平衡核間距離の 2.5 倍以上伸びると、水素分子は 2 個の水素原子に、解離した状態になっています。 原子核の空間配置は、分子構造によって、表現出来ます。 分子構造は、内部座標の数値(量)と、分子の形状や対称性(質)により、表現できます。 内部座標は、核間の結合距離や結合角などを用いて、核間の相対的な位置関係を、表現します。 2 原子分子 A-B の内部座標は、結合距離 A-B です。 3 原子分子 A-B-C の内部座標は、結合距離 A-B, B-C と、結合角 A-B-C です。 N 個の原子の分子は、N番目の原子の内部座標には、他の原子との結合距離や結合角など、3種類が必要です。 内部座標の数は、2 原子分子は 1 個、3 原子分子は 3 個です。 4 原子分子の内部座標は、3 原子分子より 3 個増加して、6 個です。 5 原子のメタン CH4 は9個、6原子のエチレン C2H4 は 12 個、12 原子のベンゼン C6H6 は 30 個です。 一般に、N 原子分子の内部座標の数は、3Nー6 個です。 3Nー6 個の内部座標に関するポテンシャル面は、HFSCF法を用いて、計算が可能です。 各内部座標に関するポテンシャル面の極小値は、分子の基底状態の分子構造である、最適化構造に対応します。 分子構造の最適化では、勾配法 ( Gradient method ) を用いて、ポテンシャル面の極小値を、検索します。 ポテンシャル面の分子の形状は、電子の波動関数に、依存します。 電子の波動関数は、それの記述に用いられる、分子軌道や電子配置に、依存します。 分子軌道は、その記述に用いられる、原子軌道に、依存します。 分子の形状は、化学結合に関与する、価電子軌道の方向性(方位)に、関連します。 価電子軌道は、H 原子は 1S 原子軌道、C, O では 2S, 2Pp 原子軌道が、関与します。 二原子分子である水素分子 H2 の内部座標は、H-H の結合距離です。 三原子分子である水分子 H2O の内部座標は、O-H の結合距離と、H-O-H の結合角です。 多原子分子のメタン CH4 の内部座標は、C-H の結合距離と、H-C-H の結合角です。 エチレン C2H4 の内部座標は、C-H, C-C などの結合距離と、H-C-H, H-C-C などの結合角です。 ベンゼン C6H6 の内部座標は、C-H, C-C などの結合距離と、H-C-H, H-C-C, C-C-C などの結合角です。 分子構造には、分子の形状や対称性など、質的な側面があります。 メタンの形状は、正四面体の中心に炭素が位置し、四つの頂点に水素が位置します。 或いは、立方体の中心に炭素が位置し、六面の対角線上に、四つの水素が位置します。 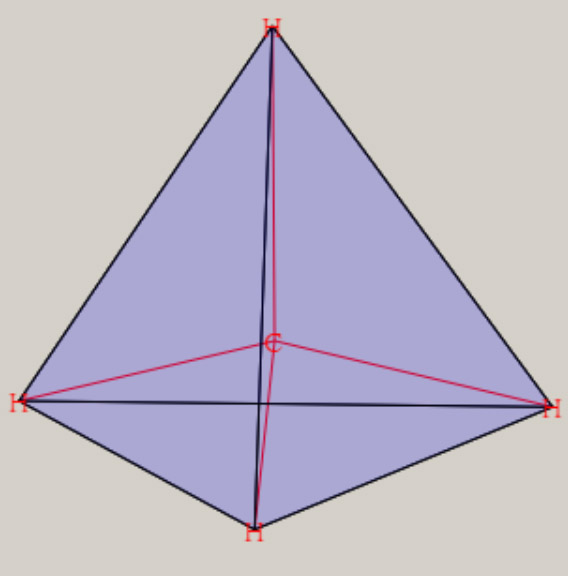 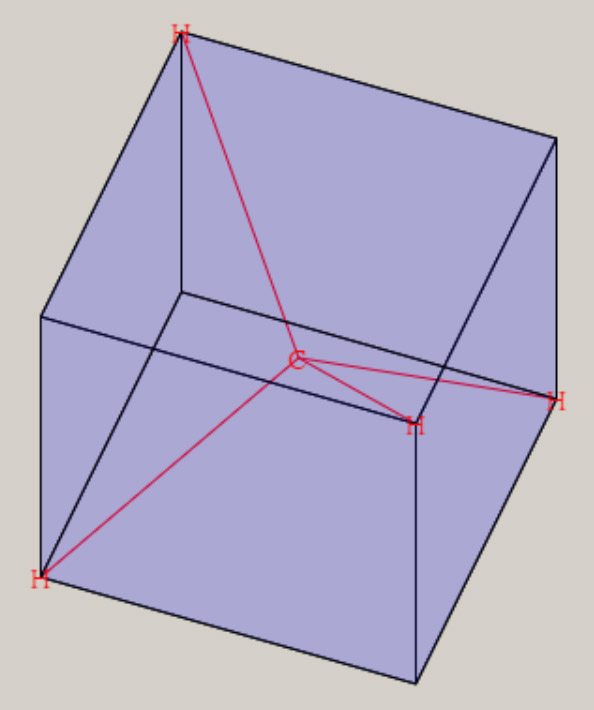
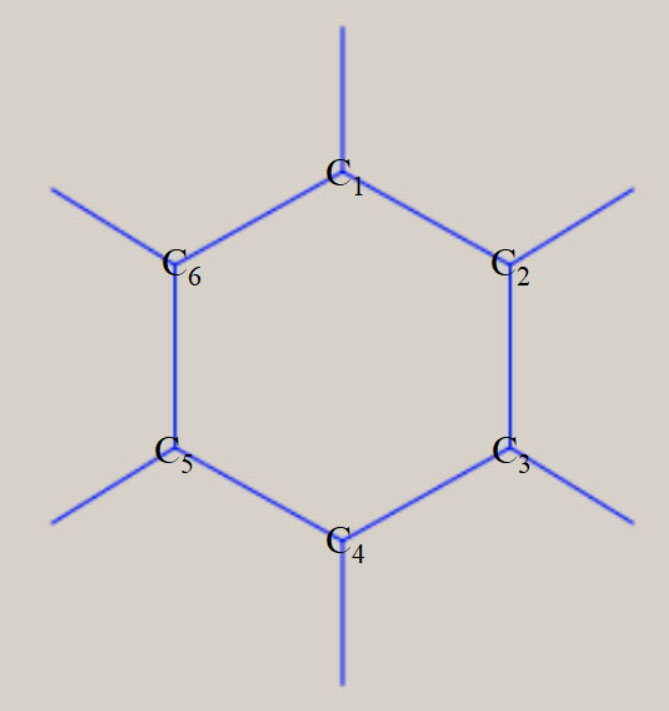
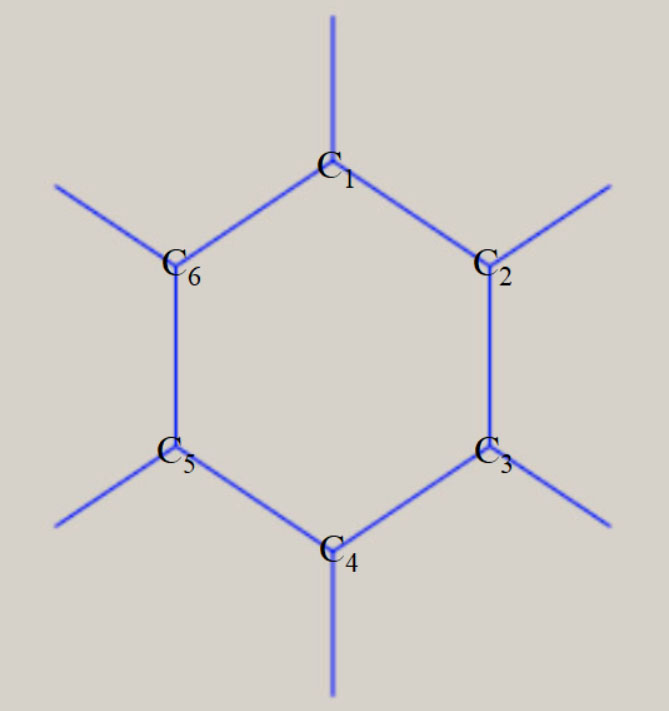
エチレンの形状は、平面の形状を持ち、六個の原子核が、同一平面上に位置します。 ベンゼンの形状は、六個の炭素原子が正六角形・6 員環の骨格をとり、六個の水素原子も六角形の形状です。 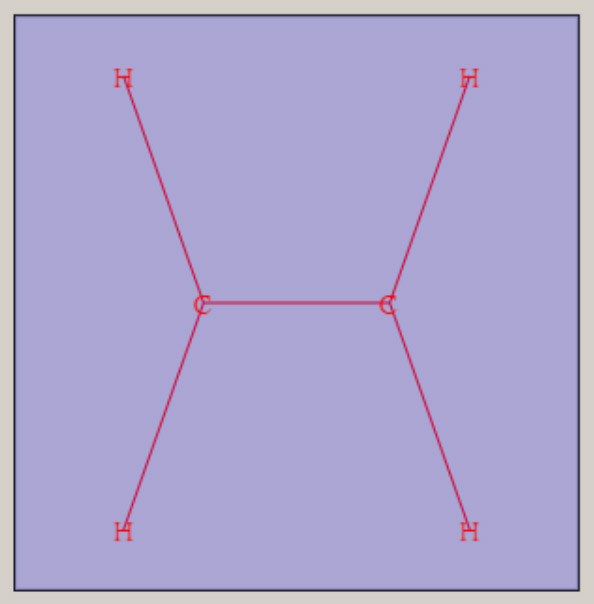 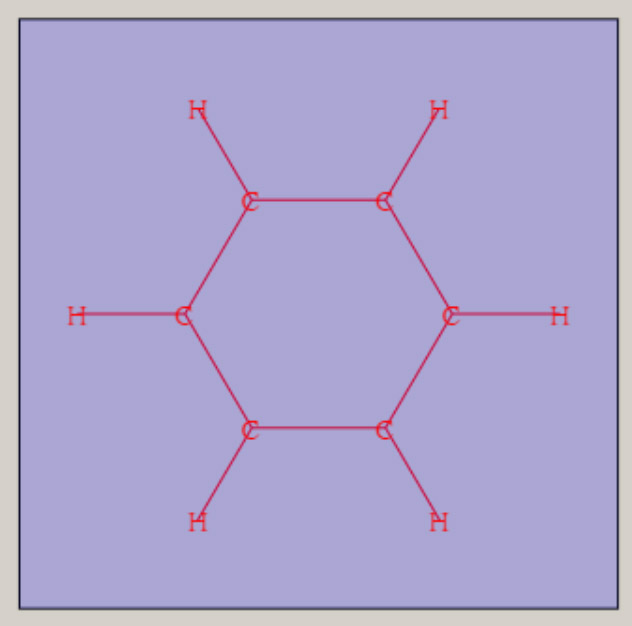
エチレンの形状は、C-C 軸の周りに、180度の回転操作( C2 )を施しても、変化しません。 C2 の様な対称操作は、それ以外に、120度の回転 ( C3 )、60度の回転 ( C6 )、があります。 さらに、対称操作として、反転操作 ( i ) や、鏡映操作 ( σh, σv, σd ) 、回映軸操作 ( s4 ) などが、あります。 分子構造の形状は、対称操作の有無に応じて、質的な区別が、可能です。 下表は、Td, C3v, C2v , D2d , D2h, D6h 対称性に関する、対称操作の有無です。
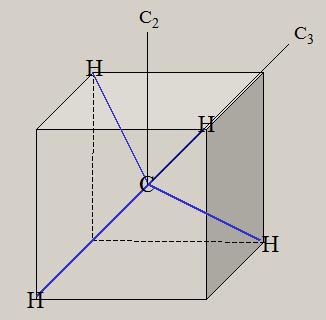
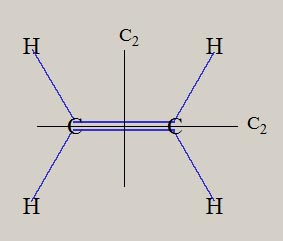
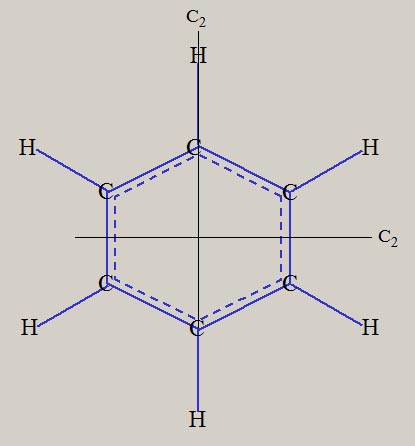
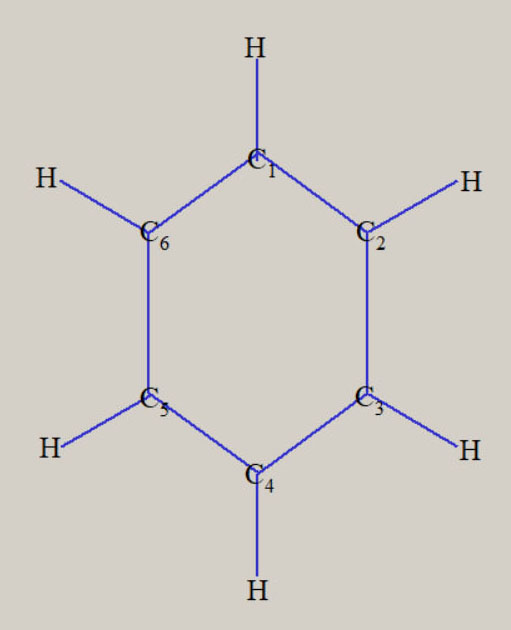
なお、何らの対称操作がない分子は、C1 です。 メタン CH4 の対称性は Td、エチレン C2H4 は D2h、ベンゼン C6H6 は D6h、です。 下図は、メタン CH4、エチレン C2H4、ベンゼン C6H6 の、分子の形状と、対称操作の一部を、示しています。
対称性を有する分子は、分子構造の表現に必要な内部座標の数は、3Nー6 個より減少します。 分子構造の表現に必要な内部座標を、全対象内部座標と、呼びます。 Td 対称性のメタンは、四つの C-H 結合距離が等しく、H-C-H の結合角は109.47°に固定されます。 従って、C-H 結合距離を全対象内部座標とすることで、分子構造が表現できます。 D2h 対称性のエチレンは、四つの C-H 結合距離が等しく、四つの H-C-C 結合角が等しくなります。 従って、全対象内部座標は、C-C 結合距離, C-H 結合距離, H-C-C 結合角の、3 種類です。 D6h 対称性のベンゼンは、六つの C-H 結合距離が等しく、六つの C-C 結合距離が等しくなります。 六つの H-C-C 結合角と、六つの C-C-C 結合角は、共に120° に固定されます。 従って、全対象内部座標は、C-C 結合距離, C-H 結合距離の、2 種類です。 対称性を有する基底状態の分子構造は、全対象内部座標に関するポテンシャル面に、依存します。 この場合、分子構造の最適化構造に必要な内部座標の数が、3Nー6 個より減少します。 メタンは 9 個が 1 個に、エチレンは 12 個が 3 個、ベンゼンは 30 個が 2 個に、減少します。 全対象内部座標
分子の対称性を考慮した分子軌道は、対称軌道 ( Symmetry Oribital ) と、呼ばれています。 Td 対称性のメタン CH4 は、a1, t2 の、各対称軌道です。 D2h 対称性のエチレン C2H4 は、b1u, b3u, ag, b2g, b2u の、各対称軌道です。 D6h 対称性のベンゼン C6H6 は、 a1g, b1u, b2u, e1u, a2u, e2g, e1g の、各対称軌道です。 なお、分子の対称性と対称軌道との関係は、数学の群論・点群の指標表 ( character table ) から、分かります。
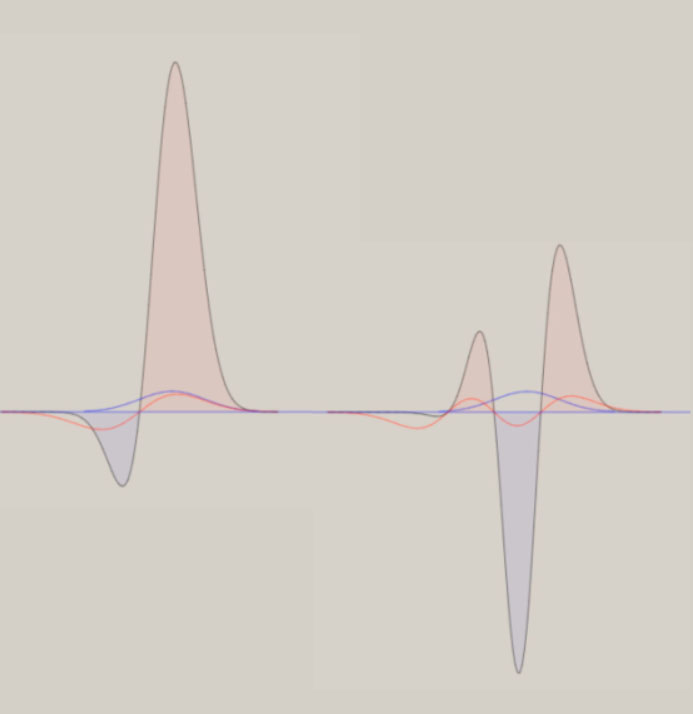
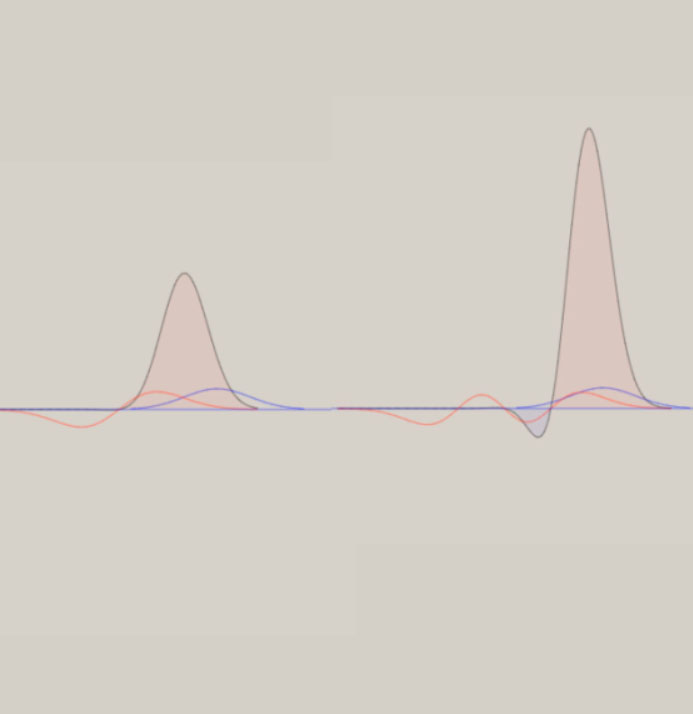
対称軌道には、量的な側面と、質的な側面の、二面があります。 量的な側面として、各対称軌道は、軌道エネルギーを持ちます。 また、異なった軌道エネルギーの対称軌道は、1a1, 2a1, 3a1, ・・・のように、自然数を付加し、表現します。 数値が小さい方の対称軌道は、より低い、軌道エネルギーを持ちます。 質的な側面として、各対称軌道は、形状があります。 a1, t2 の様に、対称軌道の名称は、対称軌道の質を、表現します。 対称軌道の性質は、原子軌道の線形結合に、依存します。 a1 軌道は、1s や2s 原子軌道が関与し、全対象の対称性を、有します。 t2 軌道は、2p 原子軌道が関与し、方向性を有し、分子のTd 対称性に、関与します。 軌道エネルギーが低い対称軌道には、内殻の原子軌道は、関与します。 軌道エネルギーが高い対称軌道には、最外殻の原子軌道が、関与します。 この対称軌道は、原子間の化学結合に関与し、価電子軌道 ( Valence Oribital ) と、呼ばれています。 対称軌道の形状は、電子密度の分布として、可視化が可能です。 下図は、エチレンと同様に、平面分子である C2Cl4 の、4b2g, 4b3u 価電子軌道の、電子密度の図です。  電子の波動関数は、対称軌道を用いた電子配置により、表現されます。 各対称軌道を占有できる最大の電子数は、t2 が 6 、e1u, e2g, e1g が各々 4 、その他は 2 です。 電子配置では、軌道エネルギーの低い対称軌道から、電子が占有していく様子を、表現します。 例えば、メタン CH4 の10個の電子は、(1a1)2・(2a1)2・(1t2)6 の、電子配置です。  下表に、 メタン, エチレン, ベンゼンの基底状態に関し、価電子軌道の電子配置を、示します。
下表は、 メタン, エチレン, ベンゼンに関し、HFSCF法で得られた、基底状態の、分子構造です。
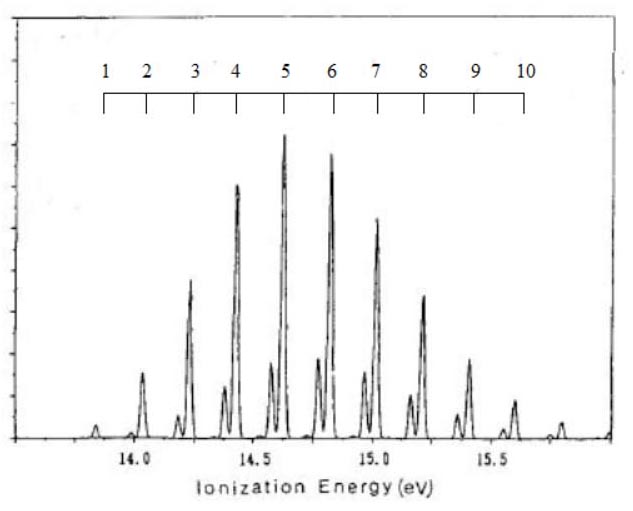
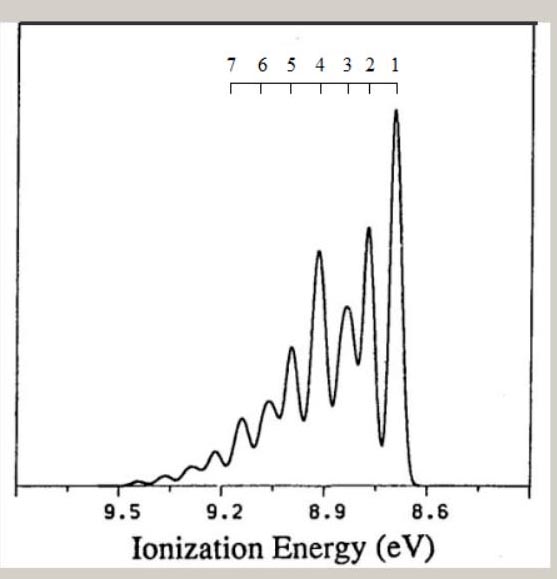
なお、分子構造の対称性より、メタンの ∠H-C-H は104.5°、ベンゼンの ∠C-C-H は120.0°です。 様々な電子配置の中で、最もエネルギーが低い状態が、基底状態です。 原子の場合、基底状態の電子配置は、H が1s1、C は1s22s22P2、です。 基底状態とは異なる、電子配置が、存在します。 H は、2s1, 2p1, 3s1,・・・、等です。 C は、1s22s22P13s1, 1s22s22P13p1, 1s22s12P23s1, ・・・、等です。 これらの電子配置の電子状態は、励起状態と、呼ばれています。 分子の場合も、様々な励起状態が、存在します。 分子の電子配置は、分子軌道・対称軌道を用いて、記述されます。 分子軌道は、分子を構成する原子の、原子軌道を用いて、記述されます。 従って、電子配置として、H の 2s,2p,3s,・・・、C の 3s,3p,4s,・・・が、関与する電子状態が、存在します。 励起状態の電子数は、基底状態の電子数と、同じです。 しかし、基底状態の電子数とは異なる、電子状態が、存在します。 例えば、10 電子のメタンの基底状態から、電子が 1 個少ない、電子状態です。 電子配置は、(1a1)2・(2a1)2・(1t2)5や、(1a1)2・(2a1)1・(1t2)6、等です。 これらの状態は、イオン化状態と、呼ばれています。 分子式は、CH4 から、 CH4+ に、変化します。 ここでは、メタン, エチレン, ベンゼンのイオン化状態に関し、電子配置や分子構造を、検討します。 メタンのイオン化状態 メタンイオン CH4+ は、メタン分子から、1個の電子が放出されると、形成されます。 メタンイオン CH4+ の電子状態は、どの対称軌道から、電子が放出されるかに、依存します。 例えば、Td 対称性では、・・・(2a1)2・(1t2)5や、・・・(2a1)1・(1t2)6、等の電子配置です。 メタンイオンの分子構造は、メタンイオンの電子状態のポテンシャル面に、依存します。 対称軌道 t2 からの電子の放出では、ヤーンテラー効果が生じることが、知られています。 ヤーンテラー効果では、Td 対称性より低い対称性の分子構造に、ポテンシャル面の極小値が、見出せます。 Td 対称性より低い対称性は、C2v, C3v, D2d の、対称性です。 より低い対称性の分子構造では、Td 対称性の対称操作の一部が欠如し、対称操作の個数が、減少します。 C2v, C3v, D2d 対称性の形状を、図示します。  分子構造の対称性の変化に伴い、全対称内部座標が、変化します。
( )内は、等価な内部座標です。 下表に、C2v, C3v, D2d 対称性のもとでの、対称軌道と電子配置を、示します。 また、電子状態の名称が、点群の指標表における、既約表現を表す記号、B1, A1, B2 を用いて、表現できます。 さらに、ダブレット( doublet )のスピン状態を、2B1 のように、左側の上付き数値 2 で、表示します。
上記の対称性・電子状態・電子配置のもとで、HFSCF法を用いて、電子の波動関数が、得れます。 さらに、勾配法で、全対称内部座標のポテンシャル面の極小値から、イオン化状態の分子構造が、得れます。 イオン化状態の量的な側面として、基底状態とのエネルギー差が、あります。 両状態間の、ポテンシャル面の極小値のエネルギー差は、断熱イオン化エネルギー ( AIE ) と、呼ばれています。 下表は、C3v, C2v, D2d の低い対称性のもとでの、 CH4+ の、AIE ( 単位:eV ) と分子構造です。
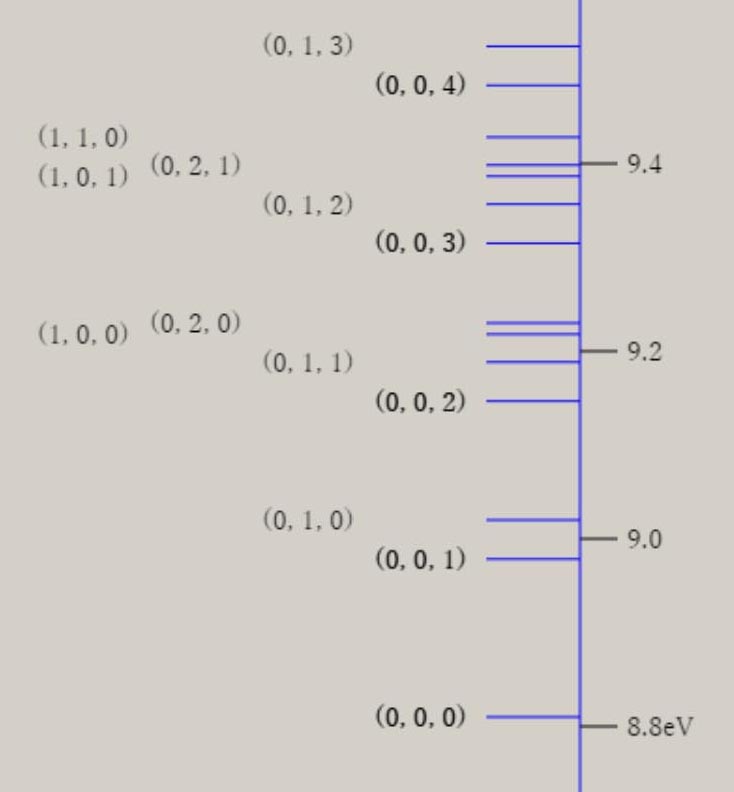
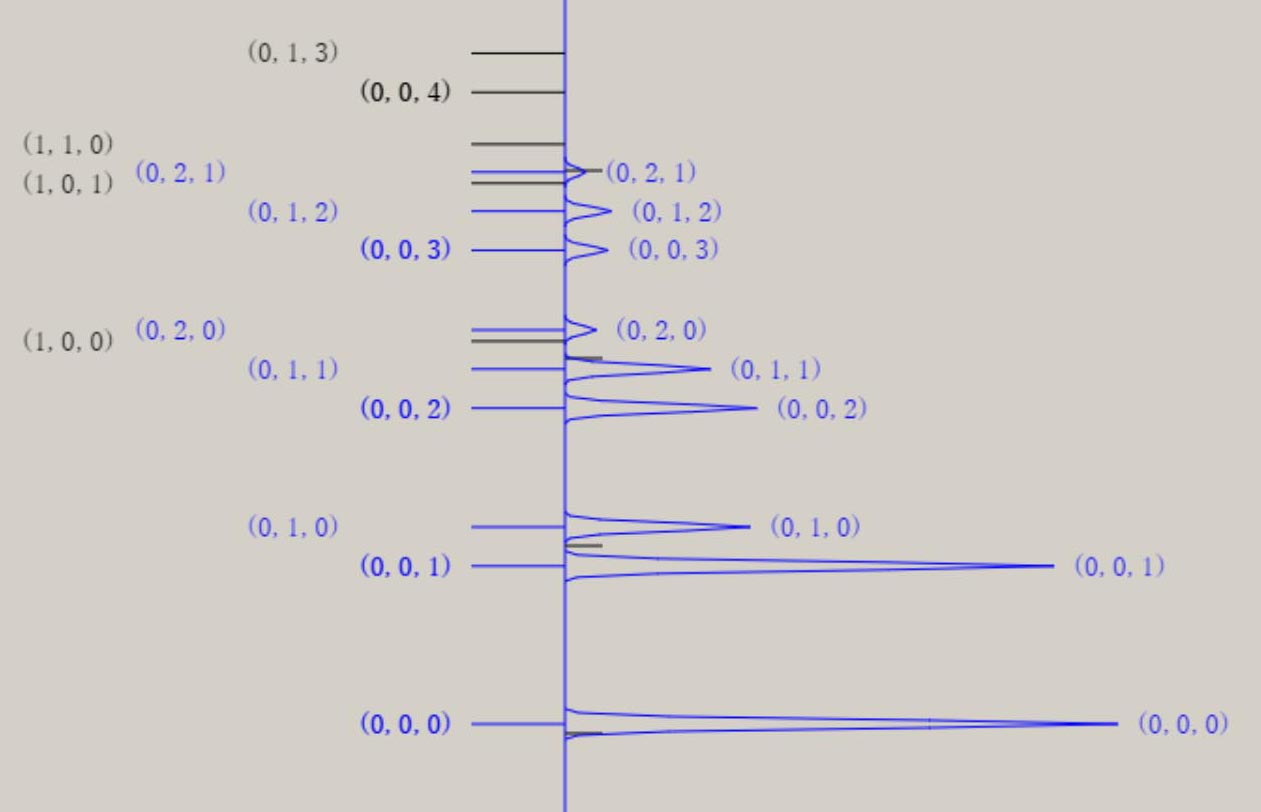
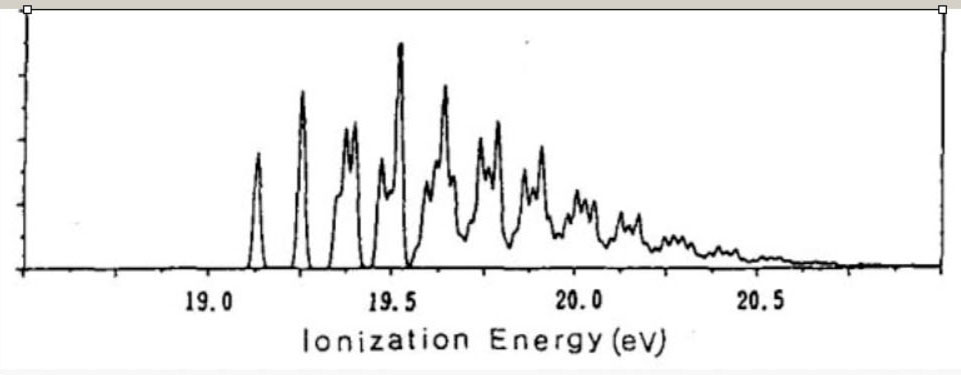
エチレンのイオン化状態 エチレンの基底状態は、・・・(2b1u)2・(1b3u)2・(3ag)2・(1b2g)2・(1b2u)2 の、電子配置です。 基底状態から、1個の電子が放出されると、エチレンイオン C2H4+ が、形成されます。 C2H4+ は、価電子軌道からの電子の放出により、D2h の対称性のもとで、以下の電子配置を、有します。
HFSCF法により、D2h の対称性のもとで、分子構造の最適化と、イオン化エネルギーの計算を、行いました。 C2H4+ の、イオン化エネルギー ( AIE ) と分子構造を、示します。
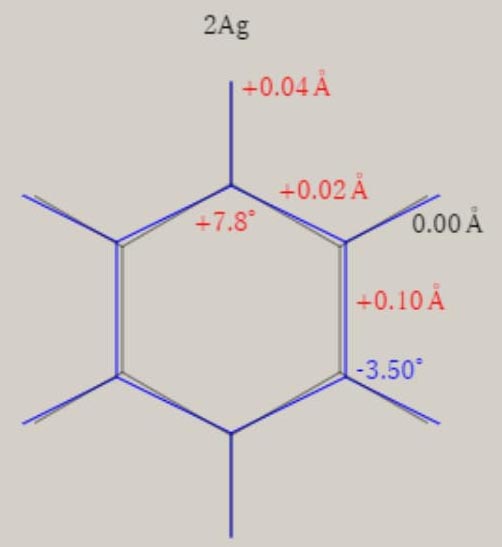
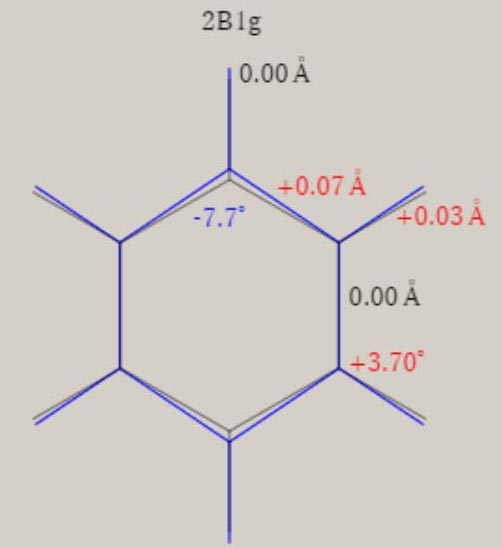
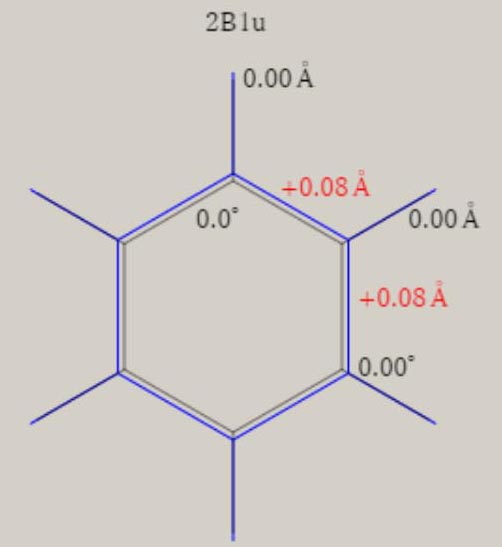
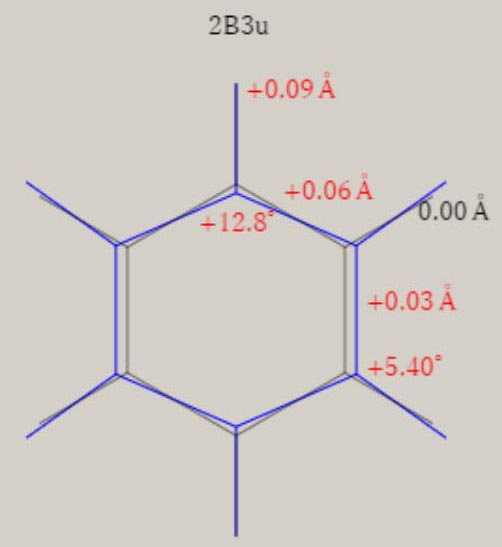
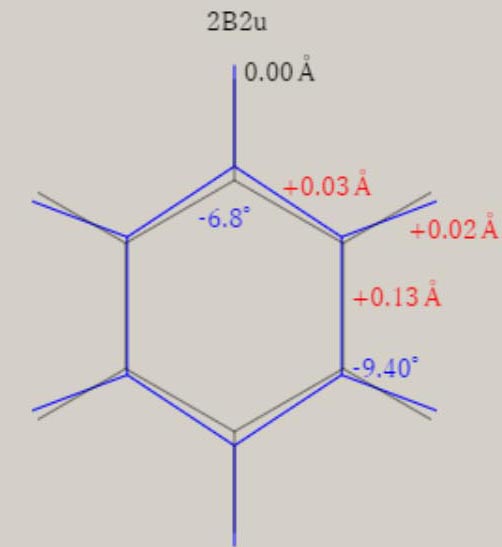
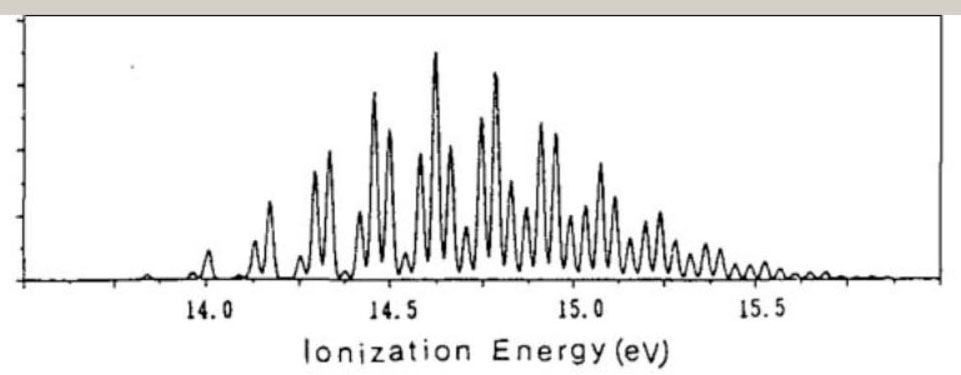
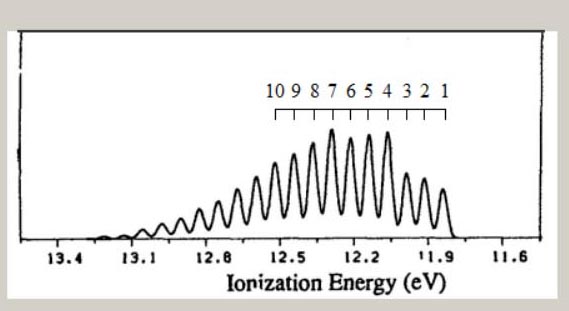
基底状態: C-C:1.32Å C-H:1.08Å ∠C-C-H:121.7° ベンゼンのイオン化状態 ベンゼンの基底状態は、D6h 対称性の分子構造を、有します。 基底状態の電子配置は、・・・(3e1u)4・(1a2u)2・(3e2g)4・(1e1g)4 です。 対称軌道 e1u, e2g, e1g からの電子の放出では、ヤーンテラー効果が、生じます。 従って、ポテンシャル面の検討には、D6h より対称性低い、D2h 対称性の分子構造を、考慮します。 D2h 対称性では、D6h 対称性が有する、6 回回転軸( C6 )が、欠如します。 D2h 低対称性では、全対称内部座標の個数は、6 個です。
下表は、D2h の低対称性のもとでの、 C6H6+ の、電子配置です。
下表は、D2h の対称性での、 C6H6+ の、AIEと分子構造です。
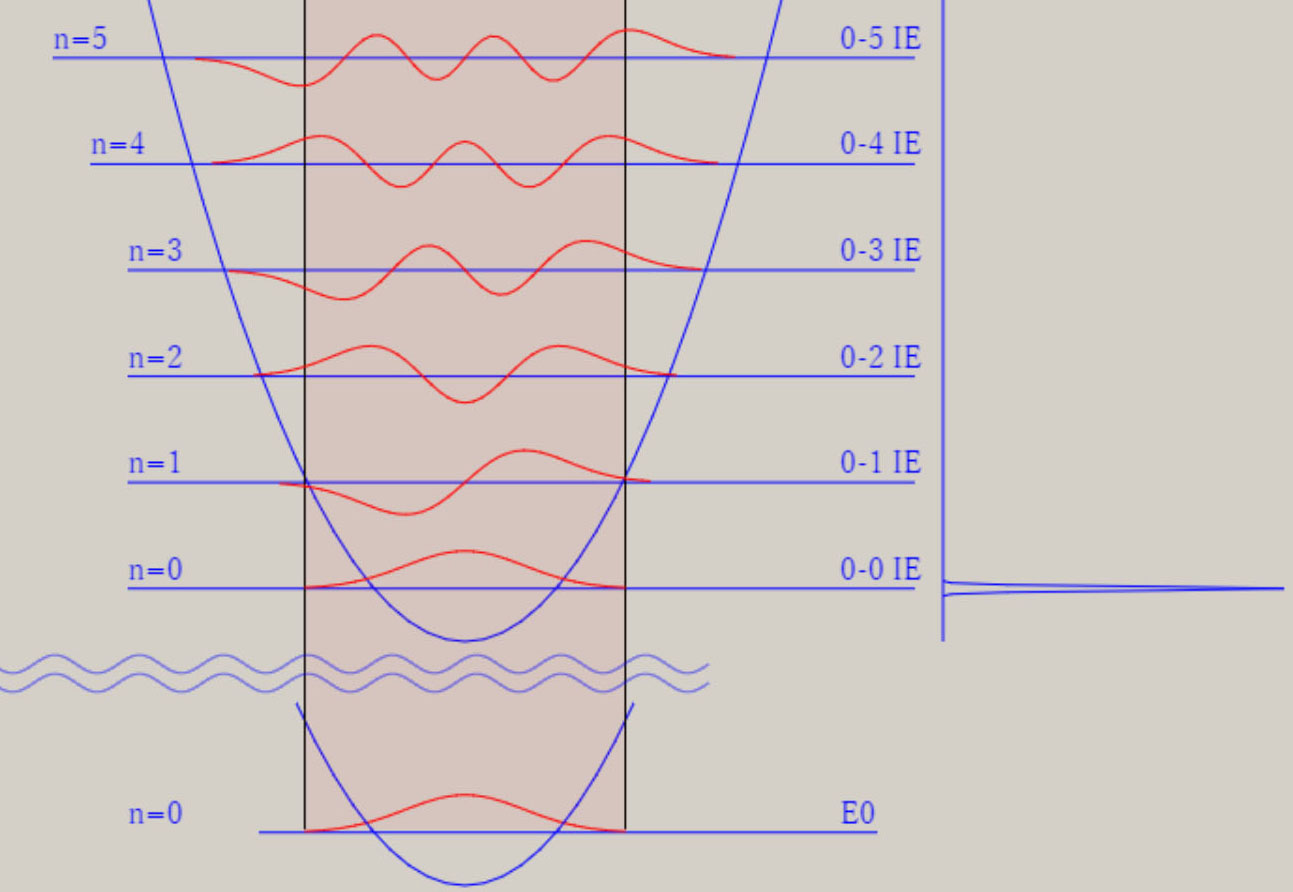
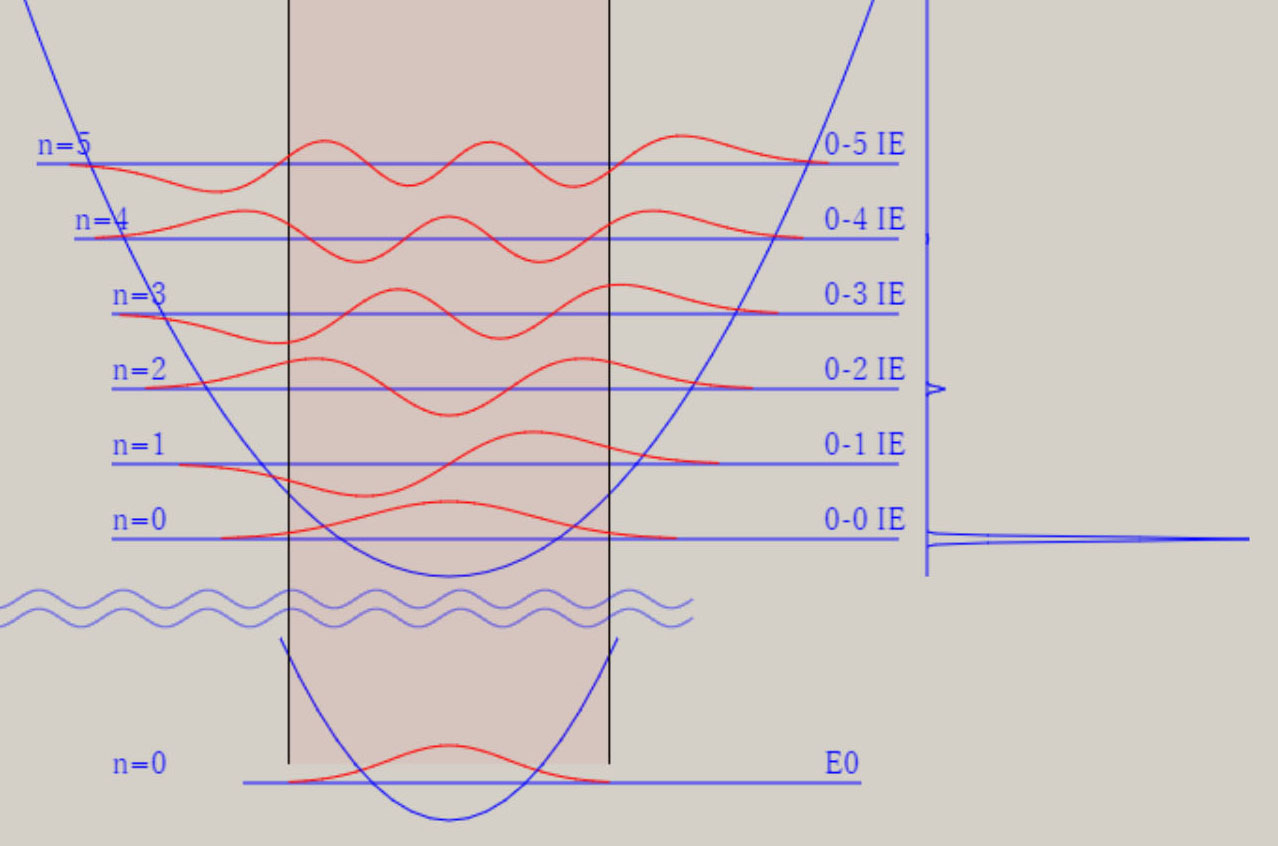
なお、2B1u の分子構造は、6 員環の骨格であり、対称性は D6h です。 分子の振動状態は、分子中の原子核の運動に対応し、ポテンシャル面の形状と、原子核の質量に、依存します。 ポテンシャル面に拘束された、原子核の運動は、振動の波動関数によって、表現されます。 一般的なポテンシャル面に関する、厳密な振動の波動関数は、求めることが、容易ではありません。 厳密な振動の波動関数は、ポテンシャル面を、二次関数で近似すると、求めることができます。 そのような波動関数の、算出方法は、調和振動子近似と、呼ばれています。 
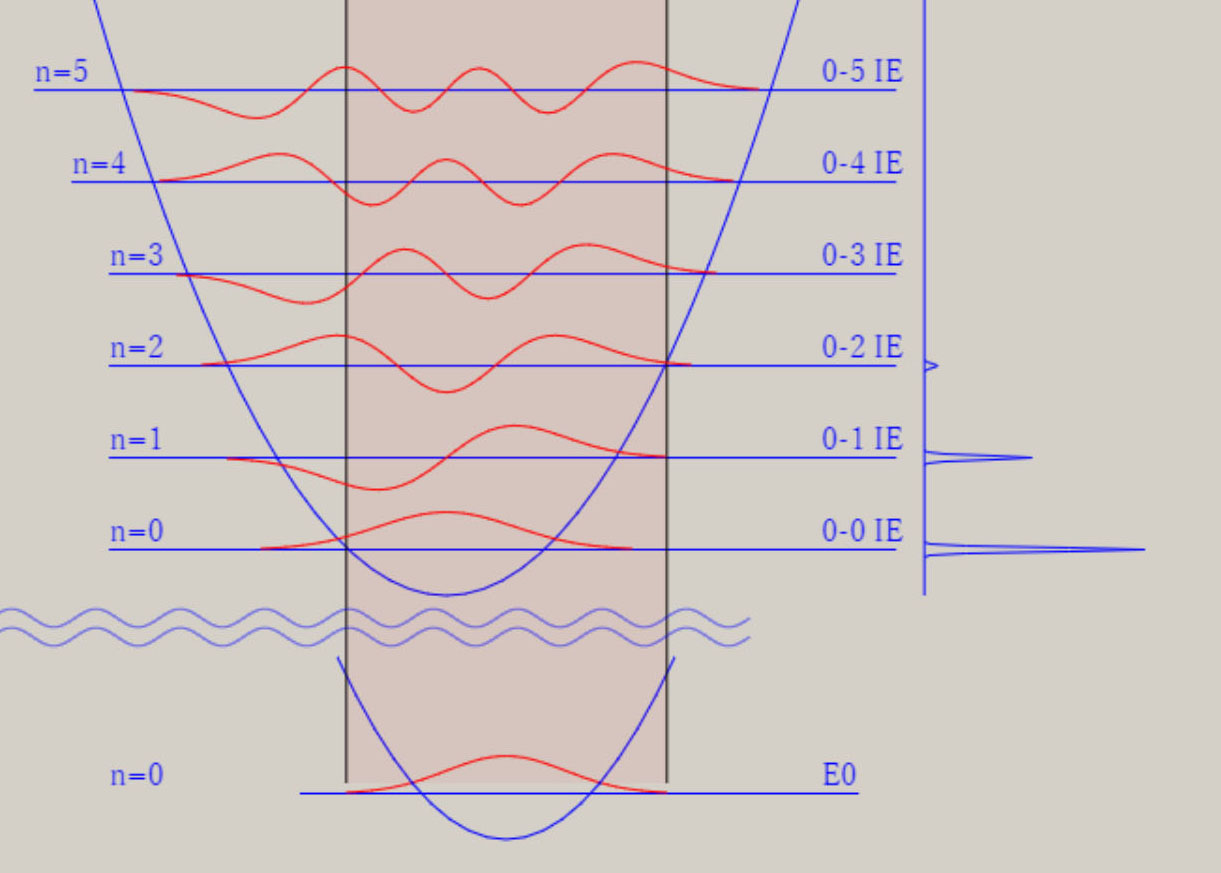
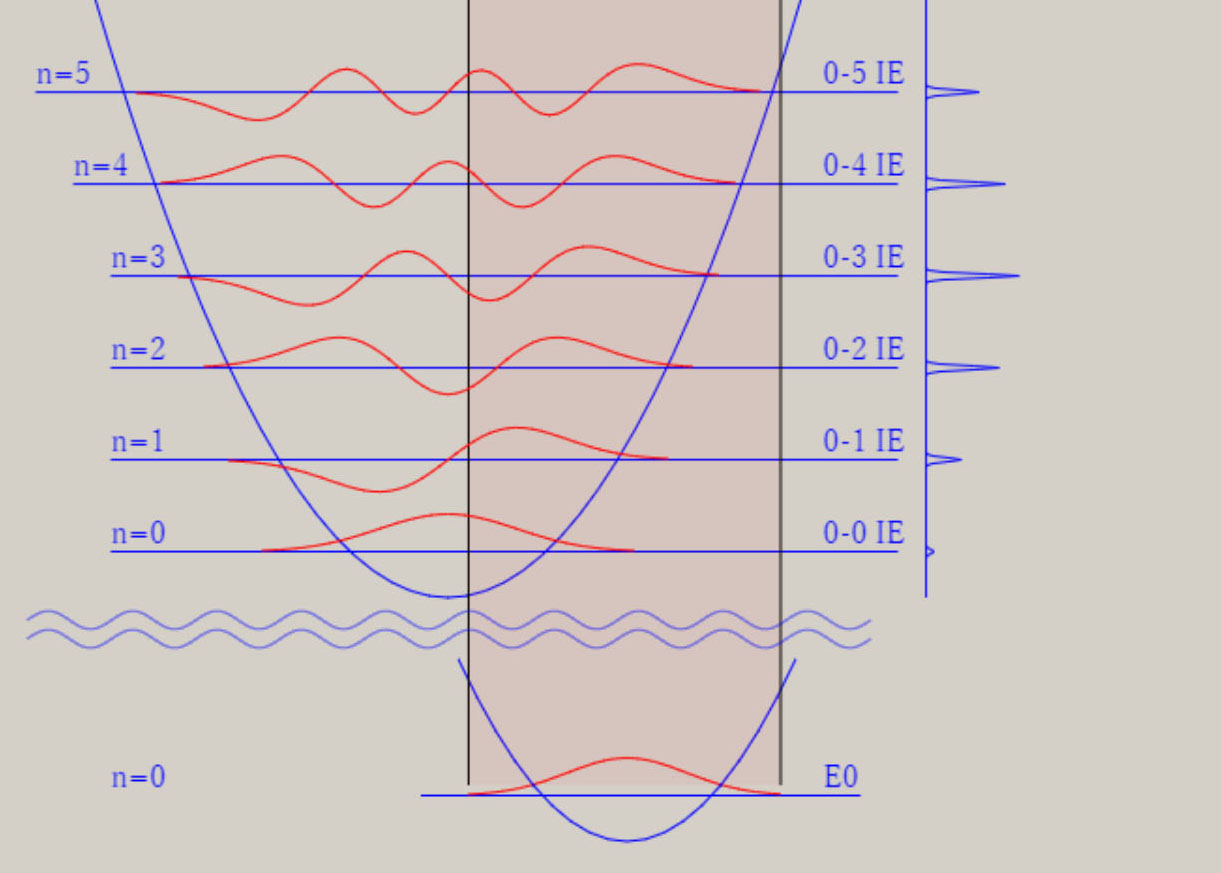
調和振動子近似 調和振動子近似を用いると、分子振動に関する、基礎的な理解を得ることが、可能です。 調和振動子近似は、格間距離に関する、ポテンシャル面 V(r) を、以下の式で、表示します。 V(r) = 1/2*k*(r-re)2 = 1/2*k*Δr2 ポテンシャル面が上式の場合、厳密なシュレーディンガー方程式の解が、得られます。 シュレーディンガー方程式の解には、量(エネルギー)と質(波動関数)の両面が、存在します。 振動のエネルギー順位 En は、次の式で、表せます。 En = (n+ 1/2)hν n は、0, 1, 2, 3, ・・・の値を取る、量子数です。 h は、プランク定数です。ν ( ギリシャ文字・ニュー ) は、振動数です。 振動のエネルギー順位は、等間隔であり、そのエネルギー差は、hν になります。 振動数 ν は、ポテンシャル面に関する力の定数 k 、換算質量 μ と、以下の式で、関連付けられます。 nν = √(k/μ) / 2π 振動数 ν は、ポテンシャル面の勾配が急なほど、即ち力の定数 k が大きなほど、大きな値を取ります。 力の定数 k が 2 倍になると、振動数は、√(2) = 1.41 倍になります。 振動数 ν は、原子量の大きな原子なほど、即ち換算質量 μ が大きなほど、小さな値を取ります。 換算質量 μ が 4 倍になると、振動数は、1/2 倍になります。 調和振動子の波動関数 ψn は、エルミート多項式を用いて、 表現できます。 下図は、振動の量子数 n に対応する、波動関数 ψn(R) を、核間距離・R の関数として、表示しています。  n=0 のとき、原子核の運動は停止しているのでなく、ゼロ点振動と呼ばれる、一定の運動をしています。 量子数 n が大きくなると、原子核の運動の領域が、拡大します。 量子数 n は、波動関数 ψ の値の符号が、変化する地点(節・ノード)の数に、一致します。 例えば、 n=0 はノード数が 0、 n=1 はノード数が 1、 n=5 はノード数が 5 が、図より読み取れます。 調和振動子近似は、モースポテンシャル面との比較から分かるように、量子数が大きな領域では、不適切です。 モースポテンシャル面は、核間距離が大きくなり、分子が解離して原子に変化する過程を、表現しています。 他方、調和振動子近似では、分子が解離していくポテンシャル面を、表現できません。 モースポテンシャル面を用いたシュレーディンガー方程式の解は、調和振動子近似のそれとは、異なります。 振動のエネルギー間隔は、等間隔ではなくなり、高いエネルギー領域になるほど、間隔は狭くなります。 振動のエネルギー順位は、量子数nに因りますが、En = (n+ 1/2)hν の式は、成立しません。 振動の波動関数は、エルミート多項式を用いた図とは、異なります。 しかし、振動の波動関数のノードの数は、量子数 n に、一致します。 振動モードと全対称振動 分子振動に関して、内部座標が2個以上の場合に関して、検討します。 水 H2O や硫化水素 H2S など、 三原子分子のポテンシャル面は、3個の内部座標によって、記述されます。 下図に、H2S のイオン化状態 2A1 に関するポテンシャル面と振動の波動関数を、表示します。 
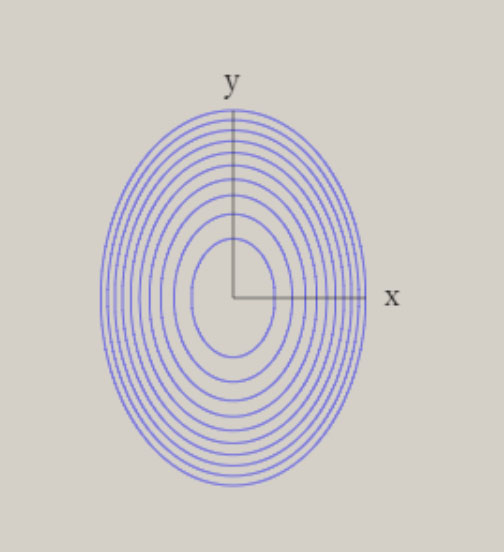
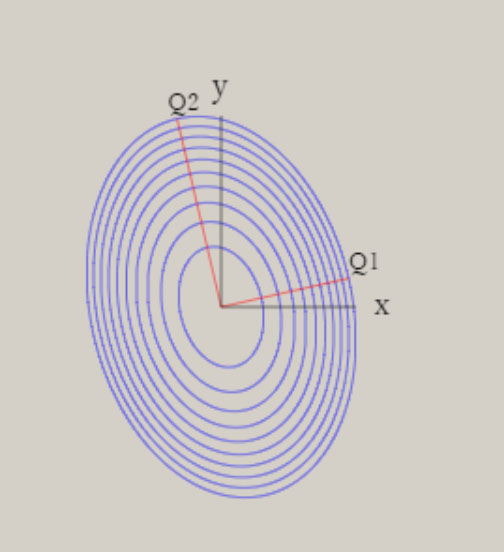
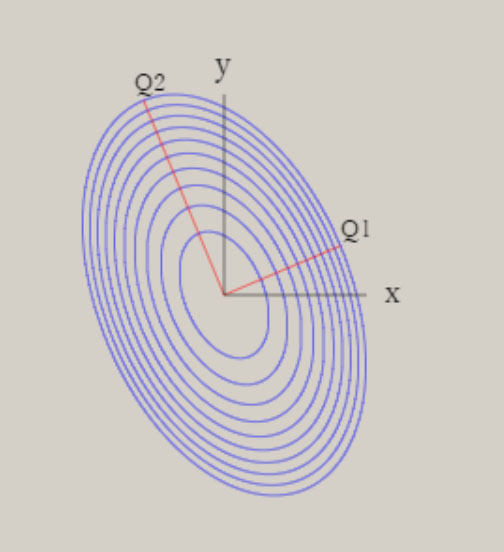
 ポテンシャル面は、全対称内部座標に関して、CI法により電子の波動関数を求め、作成しています。 上図は、H-S-H の角度に関して、80° → 180° → 280° の変化に伴うポテンシャル面を、含んでいます。 このポテンシャル面は、調和振動子では、近似できず、スプライン曲線で、近似しています。 振動の波動関数は、シュレーディンガー方程式を基礎とした、分子振動の運動方程式により、得ています。 しかし、この方法は、内部座標の数が増加するすると、取り扱いが、困難になります。 次に、ポテンシャル面を、調和振動子近似した場合に関して、検討します。 下図に、二つの内部座標に関して、ポテンシャル面の形状を、図示します。  V = x2 + xy + y2 V = 3/2*Q12 + 1/2*Q22 上記のポテンシャル面は、同一の形状を、有しています。 左図は、内部座標 x , y を用いて、V = x2 + xy + y2 の式で、表現できます。 右図は、内部座標 Q1, Q2 を用いて、V = 3/2*Q12 + 1/2*Q22 の式で、表現できます。 上記の二つの式は、Q1 = (x+y)/√(2) , Q2 = (x-y)/√(2) を用いると、一致することが、分かります。 V = 3/2*Q12 + 1/2*Q22 = 3/4*(x+y)2 + 1/4*(x-y)2 = x2 + xy + y2 なお、Q1 , Q2 は、座標軸 x, y の回転によって、表現できます。 Q1, Q2 を用いると、ポテンシャル面は、調和振動子 V = 1/2*k1*Q12 + 1/2*k2*Q22 で、近似できます。 ここで、Q1, Q2 は、基準座標と、呼ばれて、内部座標の線形結合として、表現できます。 基準座標を用いると、ポテンシャル面は、調和振動子の和としで、近似できます。 基準座標の数は、内部座標の数に、一致します。 H2S の様な、三原子分子 AB2 では、全対称内部座標として、距離 A-B と ∠B-A-B の、二つを用います。 内部座標を、x と y として、以下の式で表現できる、三種類のポテンシャル面を、検討します。 (1) V = 2*x2 + y2 (2) V = 2*x2 + y2 + 0.5*x*y (3) V = 2*x2 + y2 + x*y (1) 式は、x と y の交差項 x*y がなく、(2) 式は、交差項の係数が、0.5 、(3) 式は、交差項の係数が、1 です。 下図に、各々のポテンシャル面と、基準座標と内部座標の関係式を、示します。 さらに、 基準座標を用いた、ポテンシャル面の式を、示します。
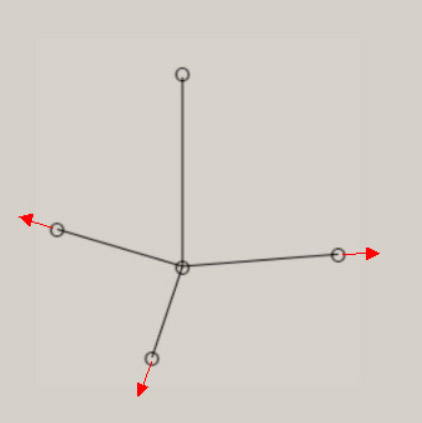
基準座標は、交差項がないポテンシャル面では、Q1 = x 、Q2 = y に、なります。 交差項があると、基準座標は、Q1 に y が、Q2 x が、含まれてきます。 基準振動は、交差項がないポテンシャル面では、距離 A-B の伸縮振動と 、∠B-A-B の変角振動に、なります。 交差項があると、基準振動には、伸縮振動と変角振動の、coupling(連結)が、見出されます。 振動の波動関数は、個々の基準座標毎に、調和振動子近似で、基準振動として、表現できます。 振動状態は、振動の量子数 n1, n2 を用いて、(n1, n2) で、指定できます。 また、振動の全波動関数は、基準振動の重ね合わせで、表現できます。 振動のエネルギー値は、基準座標毎に、E1 = (1/2 + n1)hν1 , E2 =(1/2 + n2)hν2 で、表現できます。 ν1, ν2 は、基準振動数と、呼ばれています。 振動状態 (n1, n2) の全エネルギー値は、、E1 = (1/2 + n1)hν1 +(1/2 + n2)hν2 に、なります。 基準振動数の観測値は、赤外線吸収スペクトルより、求まります。 基準振動の波動関数は、エルミート多項式を用いて、表現できます。 その形状は、先に図示した、二原子分子の場合と、同じです。 また、振動に伴う分子構造の変化を、振動モードとして、表現できます。 3原子分子の振動モードの近似的な形は、下図のように、表示できます。 全対称伸縮振動 (A1) 全対称変角振動 (A1) 逆対称伸縮振動 (B1) 
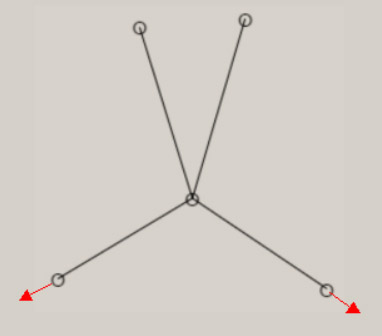
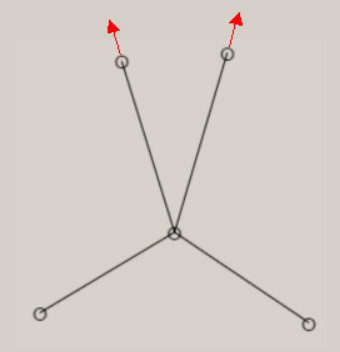
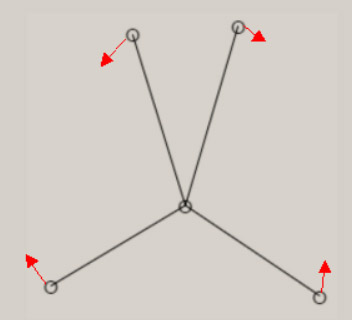
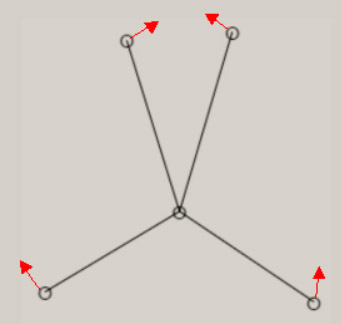
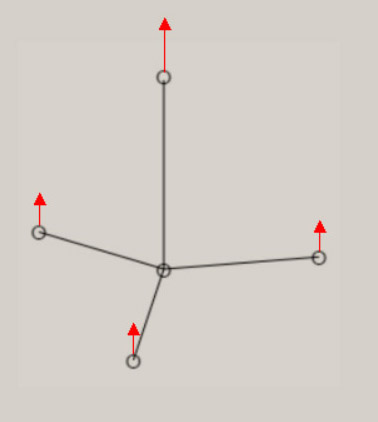
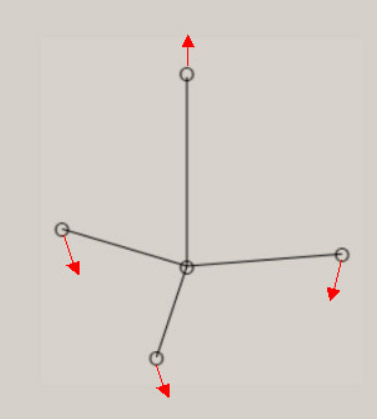
振動に伴う分子構造の変化の様子は、伸縮振動や変角振動のように、振動モードの名称に、付加されています。 分子が対称性を有する場合、振動モードは、分子の対称性を、反映しています。 振動モードの名称に、点群の指標表における、既約表現を表す記号を、A1, B1 のように、用います。 A1 モードは、全対称振動と呼ばれ、振動に伴う分子構造の変化において、分子の対称性が保持されます。 振動モードの数は、基準振動の数、基準座標の数、内部座標の数に、一致します。 全対称振動の振動モードの数は、全対称内部座標の数に、一致します。 全対称内部座標の線形結合で、全対称基準座標が、表現できます。 基底状態の全対称基準振動の振動モードと振動数 基底状態のメタン, エチレン, ベンゼンに関し、全対称基準振動の近似的な振動モードの形を、図示します。 さらに、振動数 ( cm-1 ) に関し、計算値と観測値を、示します。 メタン CH4
エチレン C2H4
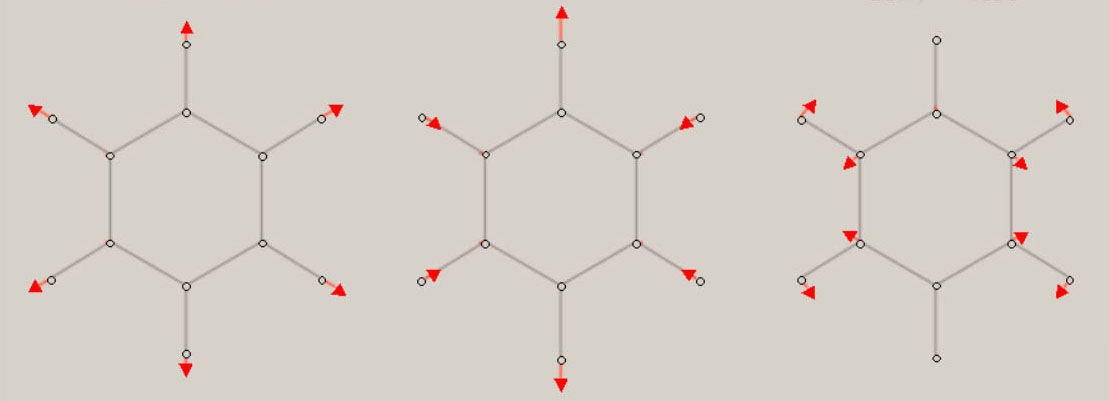
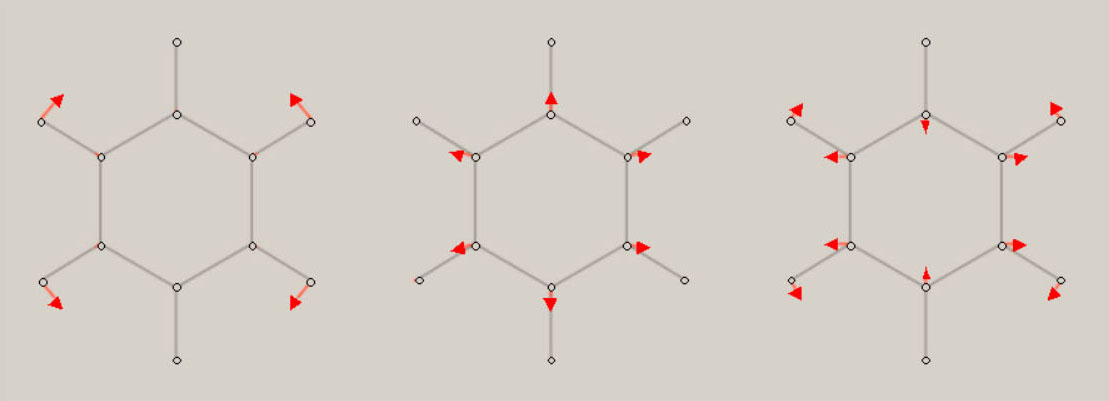
ベンゼン C6H6
イオン化状態の全対称基準振動の振動モードと振動数 ( cm-1 ) イオン化状態のメタン, エチレン, ベンゼンに関し、全対称基準振動の近似的な振動モードの形を、図示します。 さらに、振動数 ( cm-1 ) に関し、計算値を、示します。 メタン CH4+
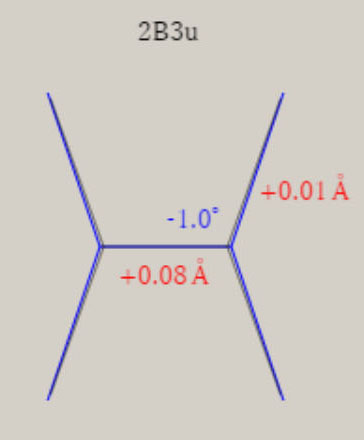
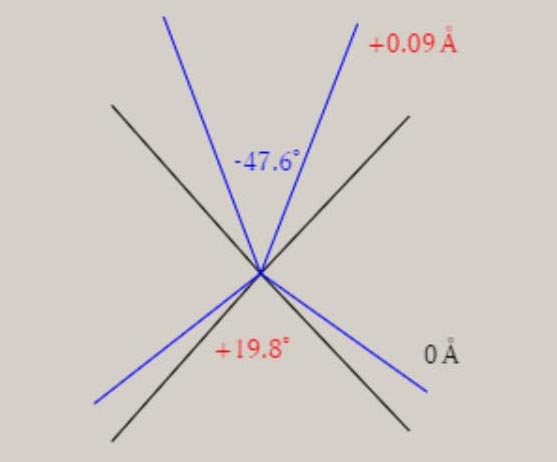
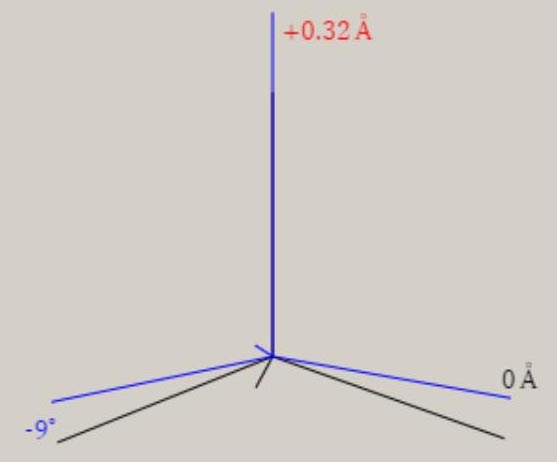
エチレン C2H4+ D2h 対称性の分子構造
2B3u状態
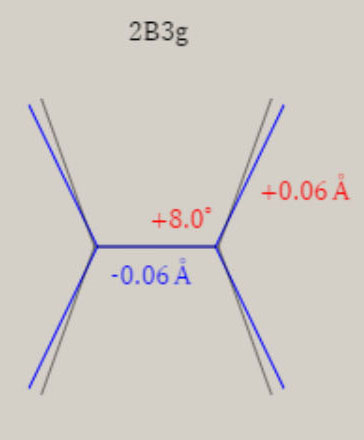
2B3g状態
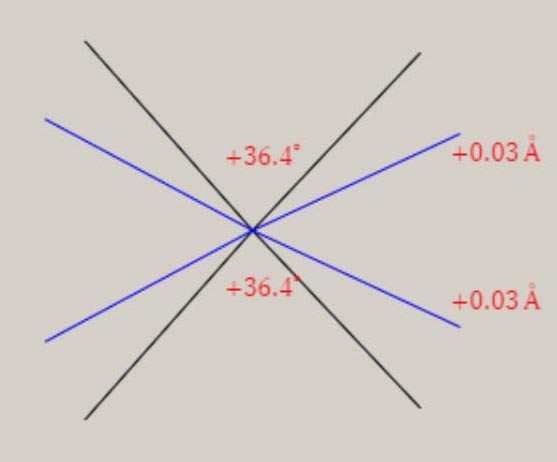
2Ag状態
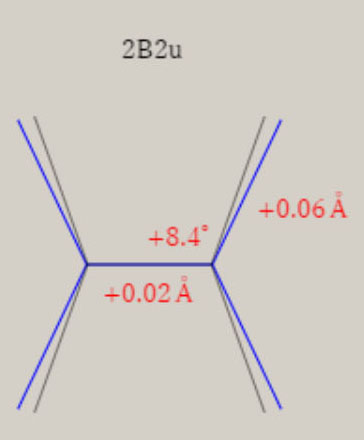
2B2u状態
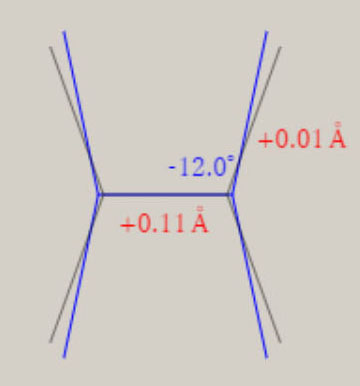
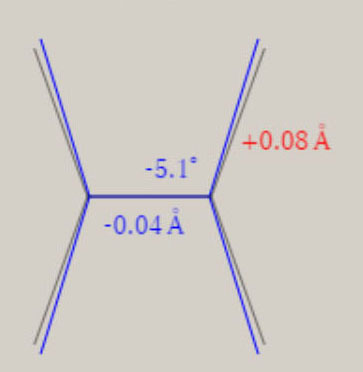
2B1u状態
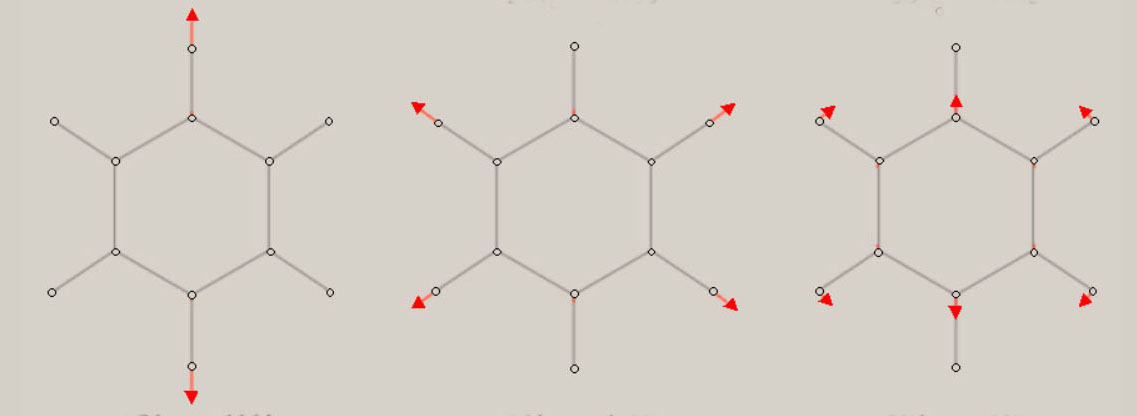
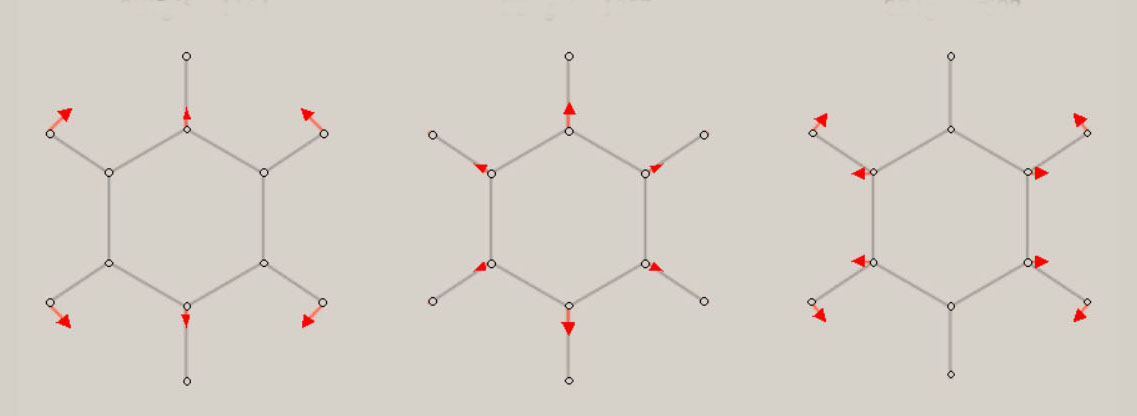
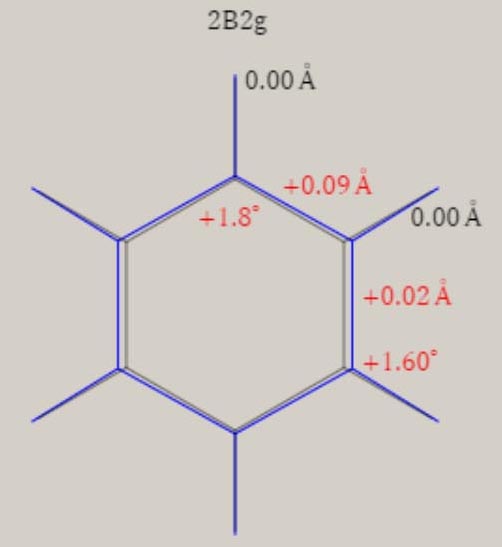
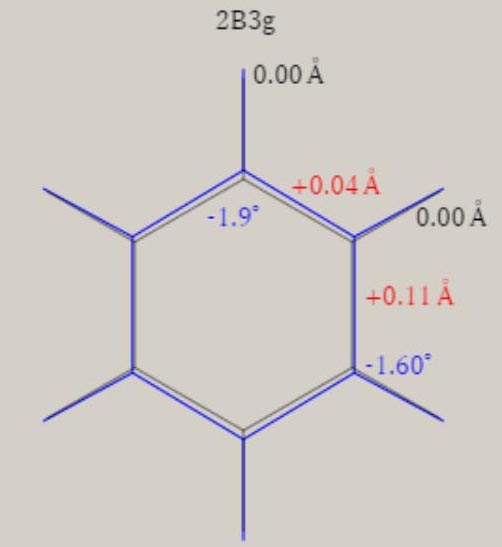
ベンゼン C6H6+ D6h 対称性の分子構造 電子状態は、2A1g
D2h 対称性の分子構造 |















 1230
1230